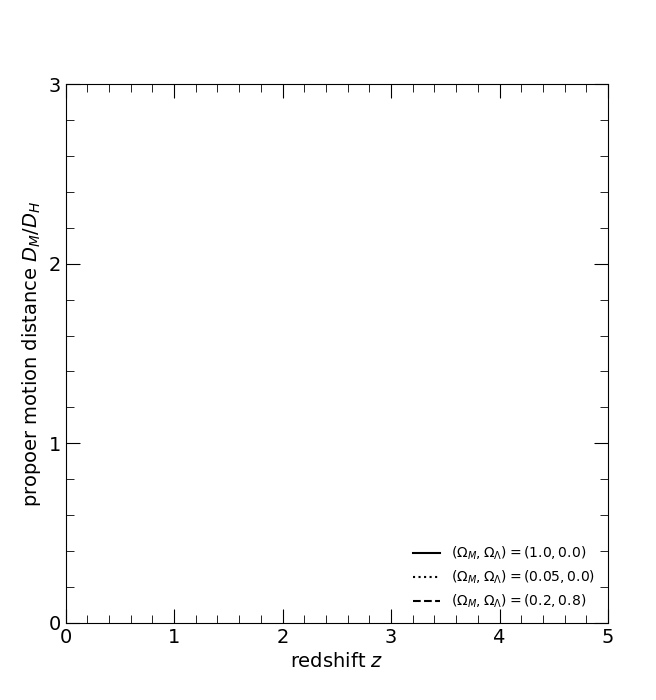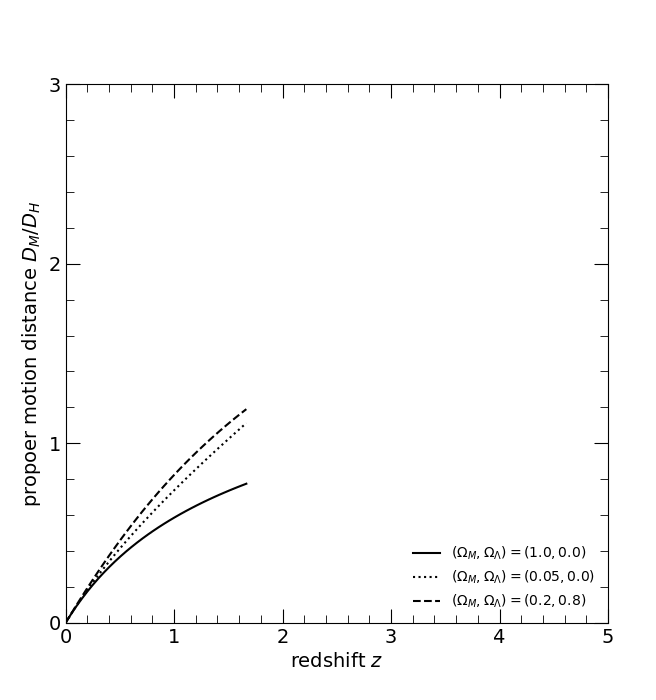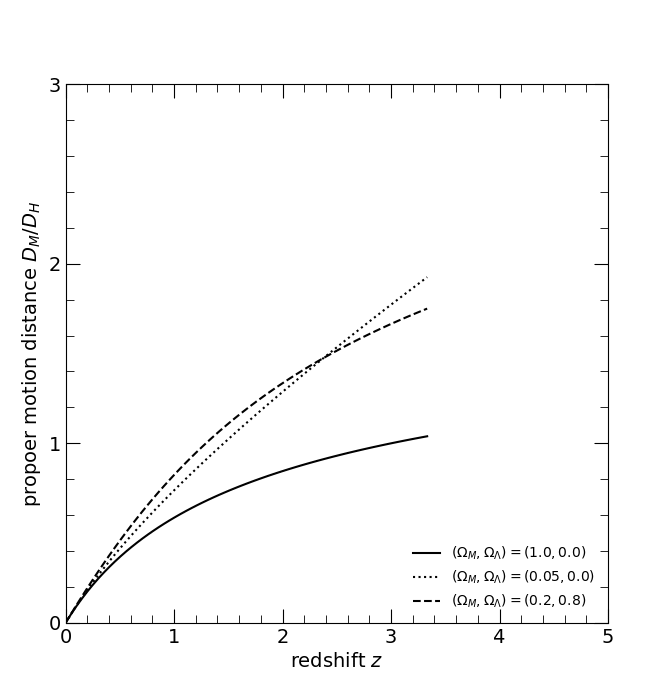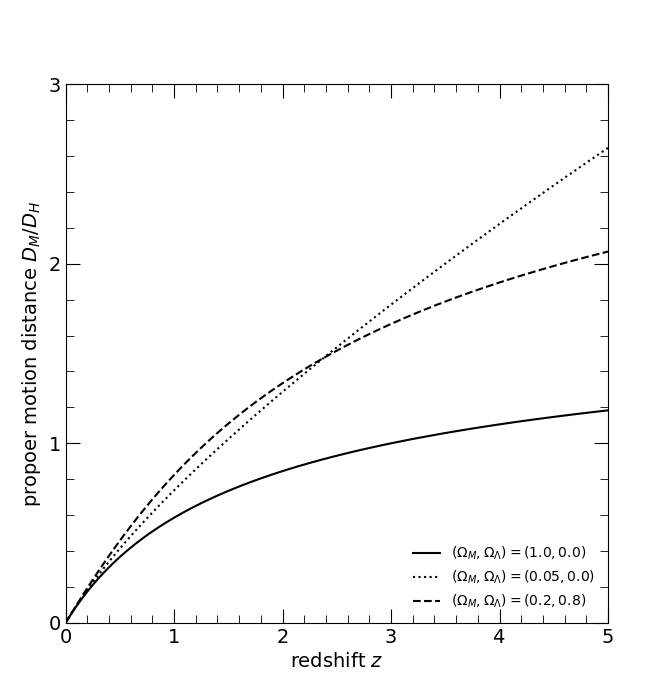
The dimensionless proper motion distance DM/DH. The three curves are for the three world models, Einstein-de Sitter (ΩM, ΩΛ) = (1, 0), solid; low-density, (0.05, 0), dotted; and high lambda, (0.2, 0.8), dashed.
Hogg, D. W. (2000)
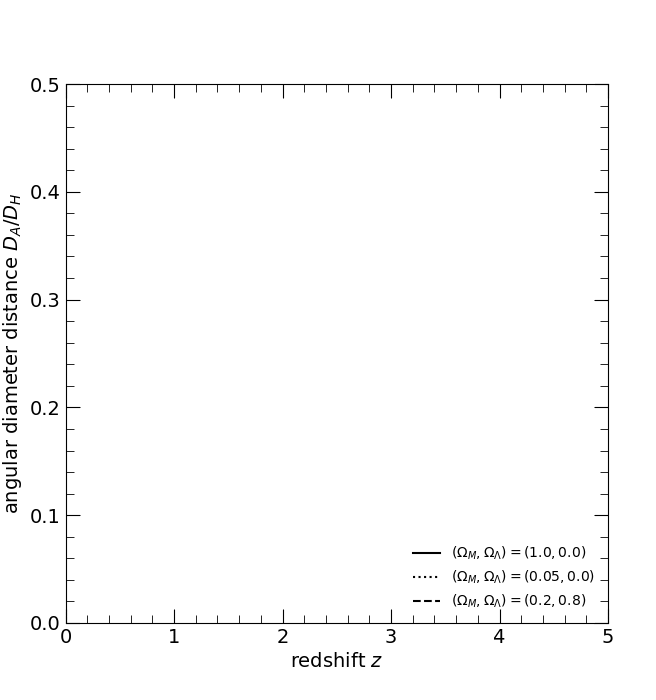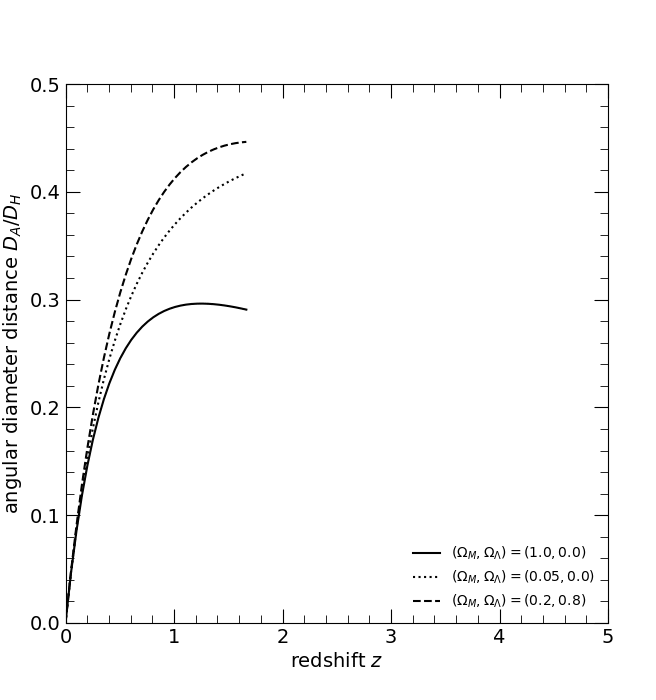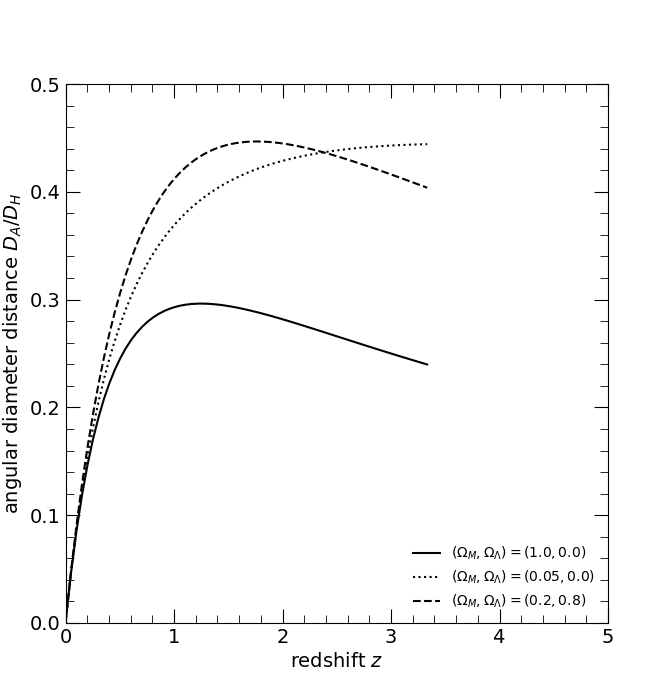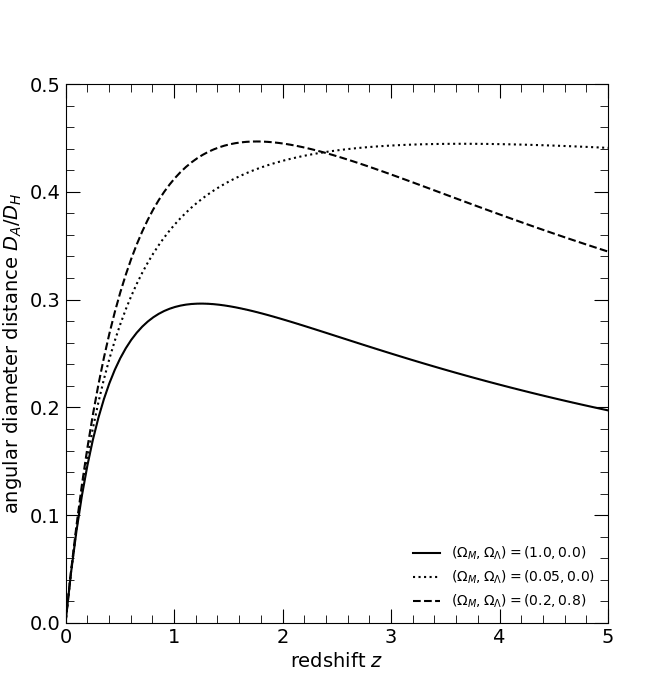
The dimensionless angular diameter distance DA/DH. The three curves are for the three world models, (ΩM, ΩΛ) = (1, 0), solid; (0.05, 0), dotted; and (0.2, 0.8), dashed.
Hogg, D. W. (2000)
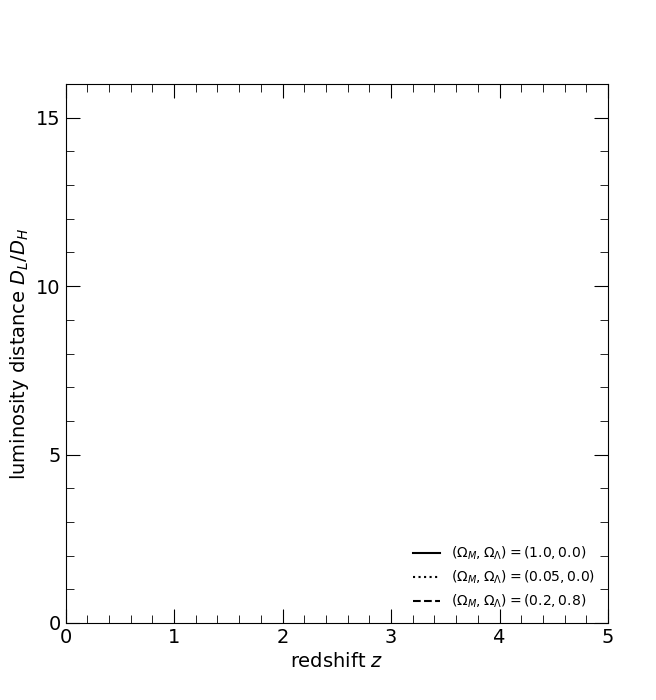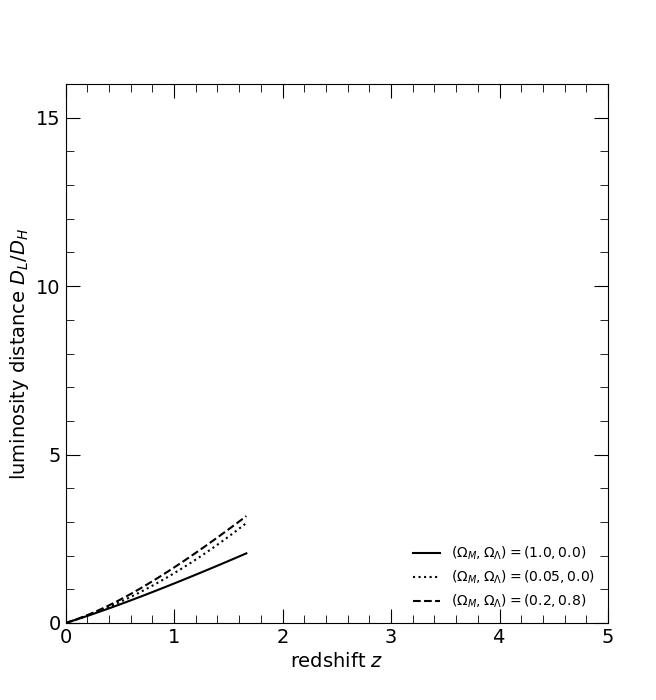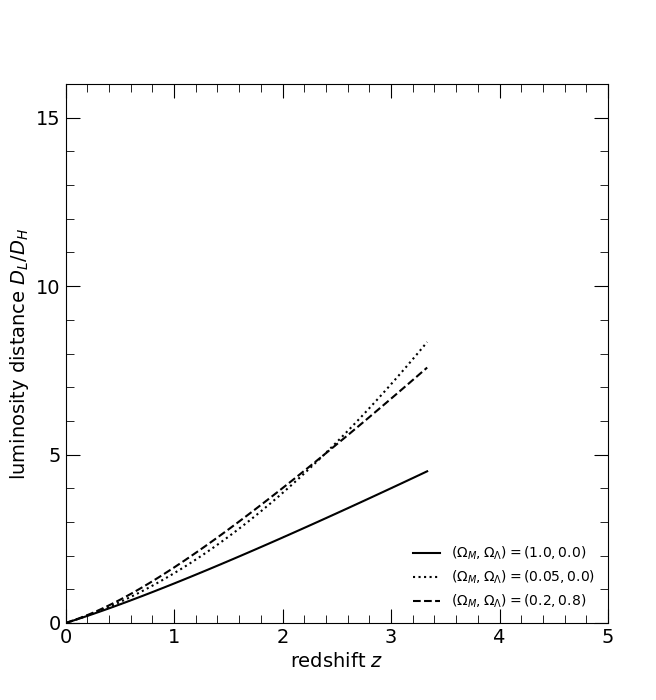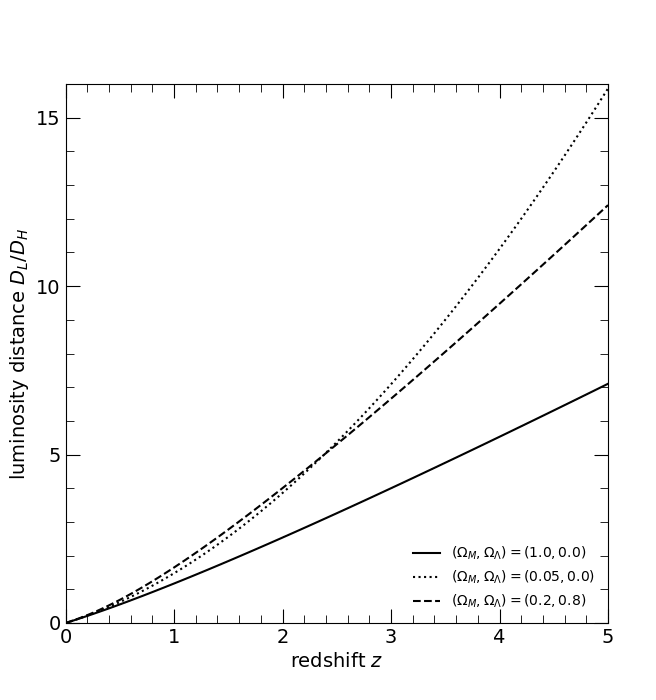
The dimensionless luminosity distance DL/DH. The three curves are for the three world models, (ΩM, ΩΛ) = (1, 0), solid; (0.05, 0), dotted; and (0.2, 0.8), dashed.
Hogg, D. W. (2000)
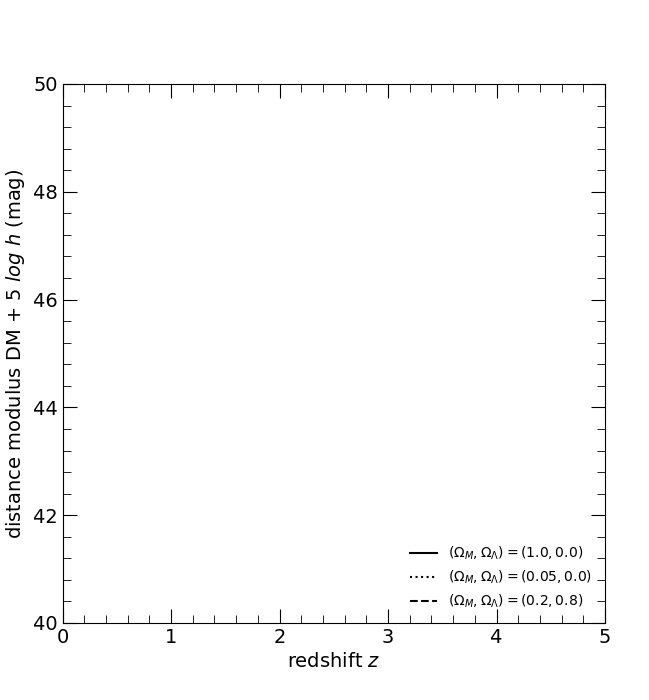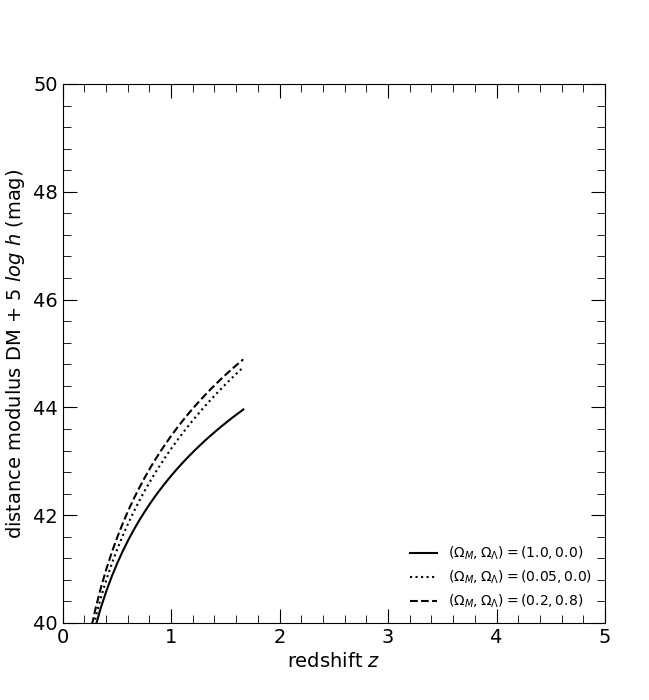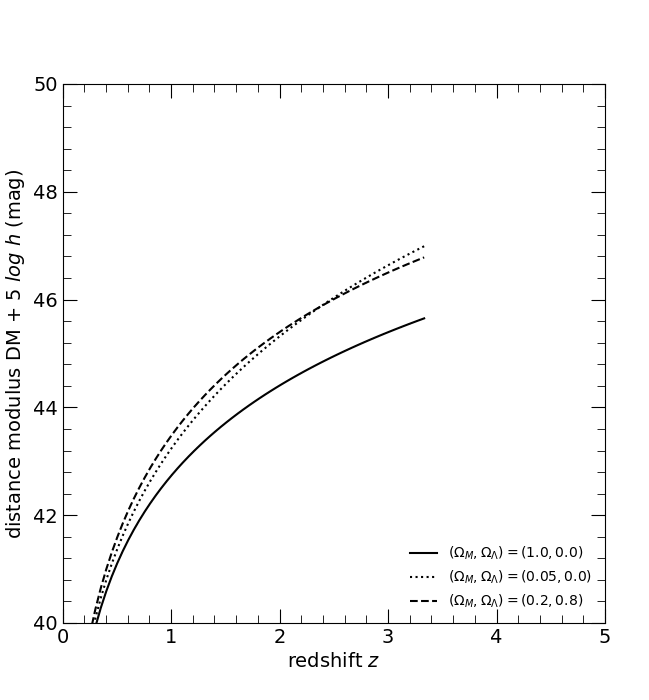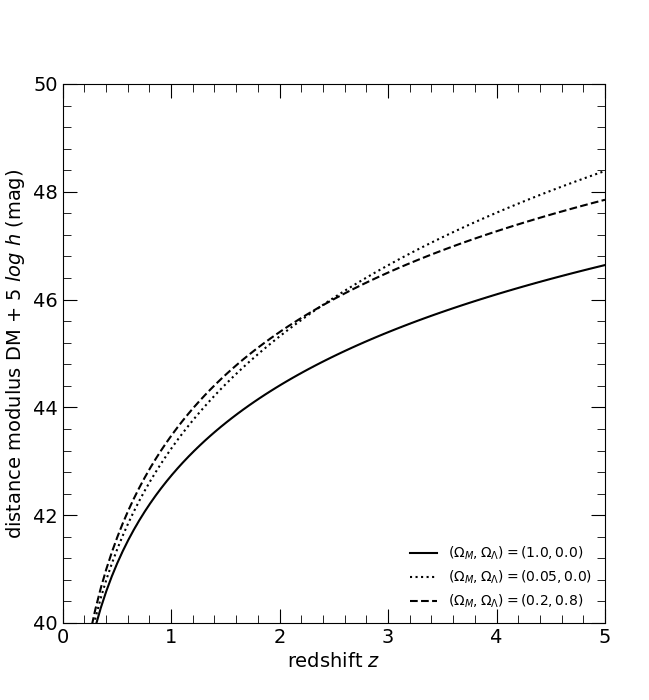
The distance modulus DM. The three curves are for the three world models, (ΩM, ΩΛ) = (1, 0), solid; (0.05, 0), dotted; and (0.2, 0.8), dashed.
Hogg, D. W. (2000)
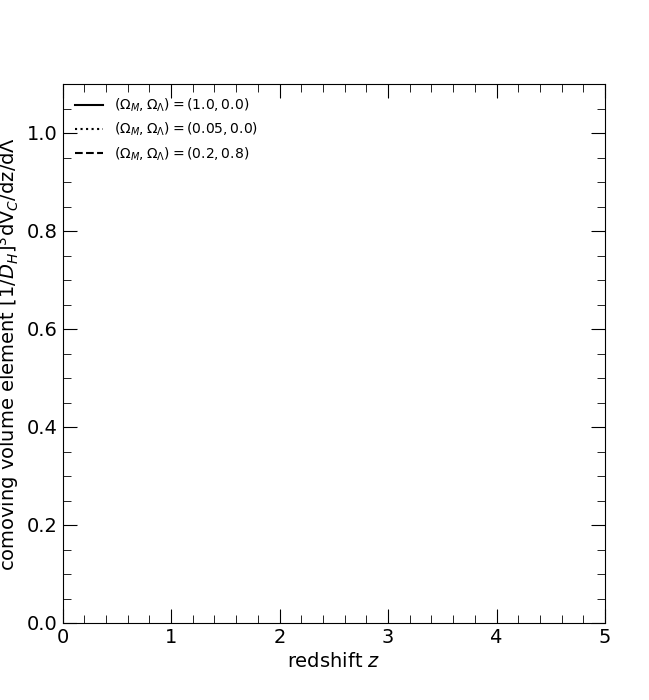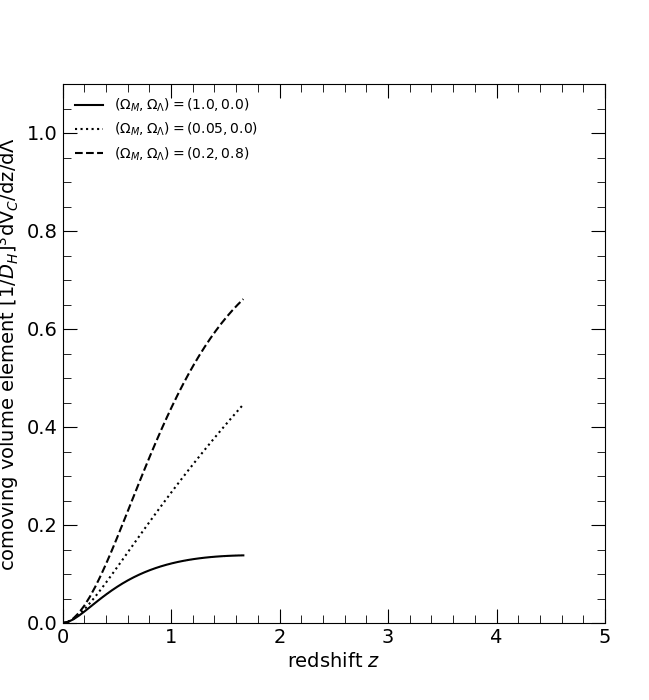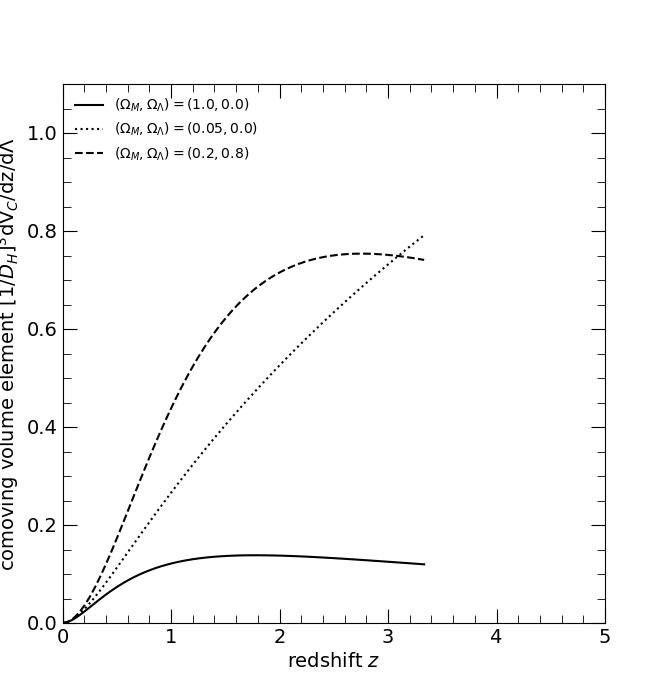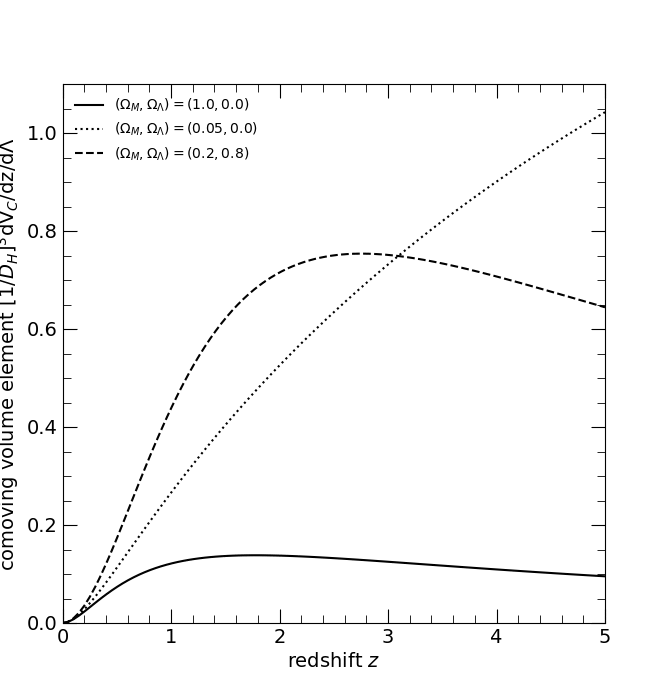
The dimensionless comoving volume element (1/DH)3 (dVC/dz). The three curves are for the three world models, (ΩM, ΩΛ) = (1, 0), solid; (0.05, 0), dotted; and (0.2, 0.8), dashed.
Hogg, D. W. (2000)
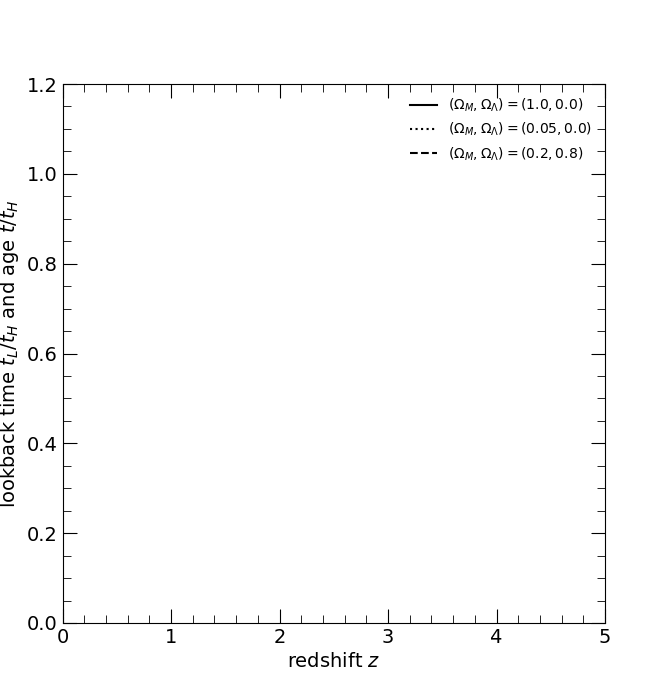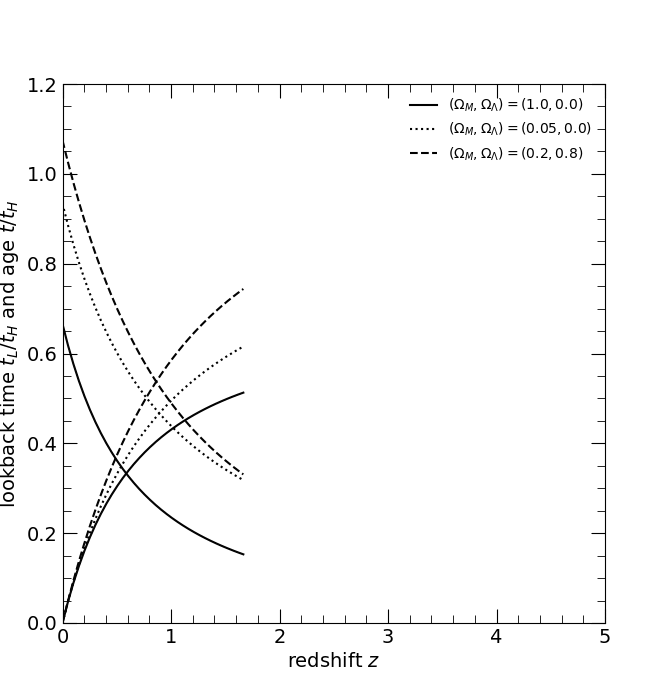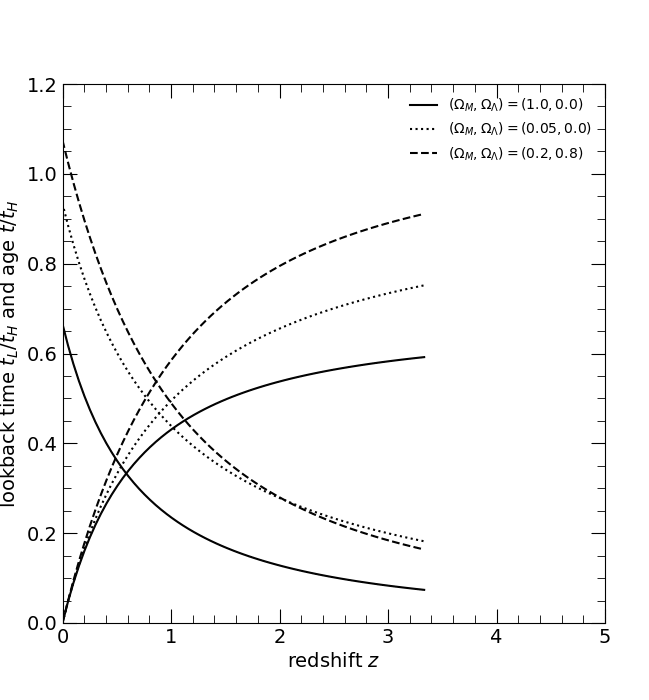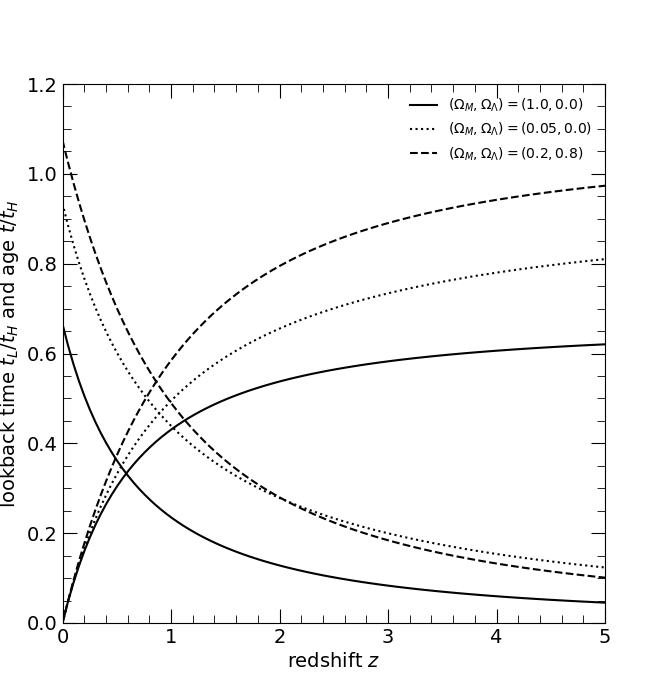
The dimensionless lookback time tL/tH and age t/tH. Curves cross at the redshift at which the Universe is half its present age. The three curves are for the three world models, (ΩM, ΩΛ) = (1, 0), solid; (0.05, 0), dotted; and (0.2, 0.8), dashed
Hogg, D. W. (2000)
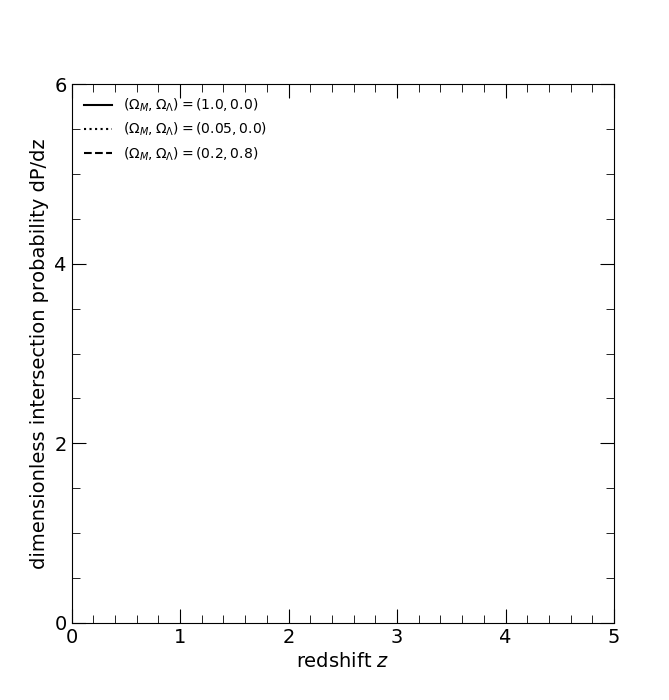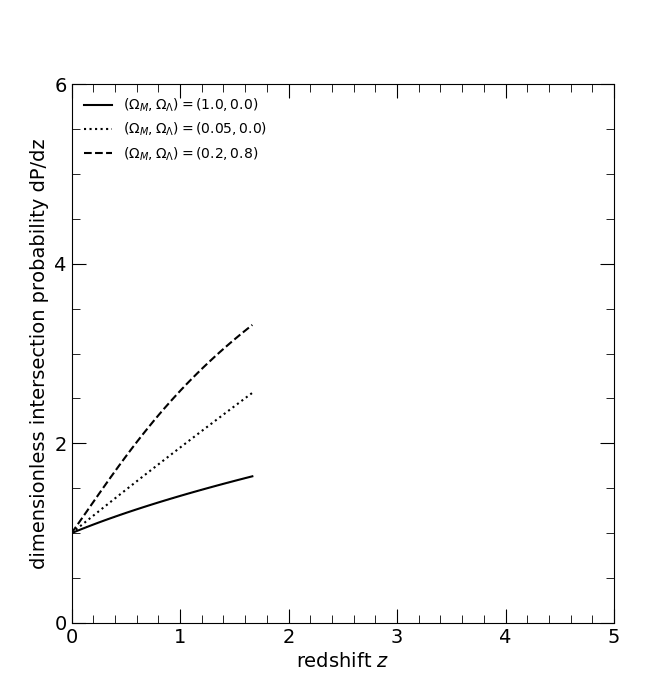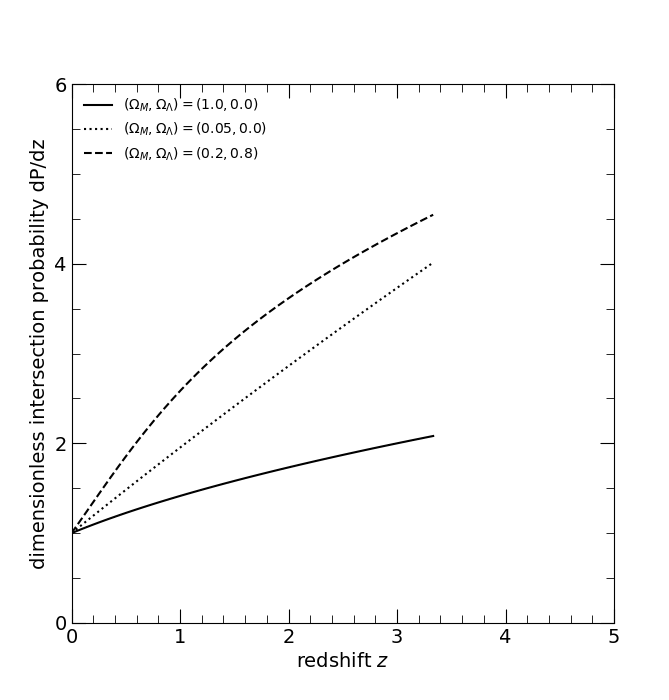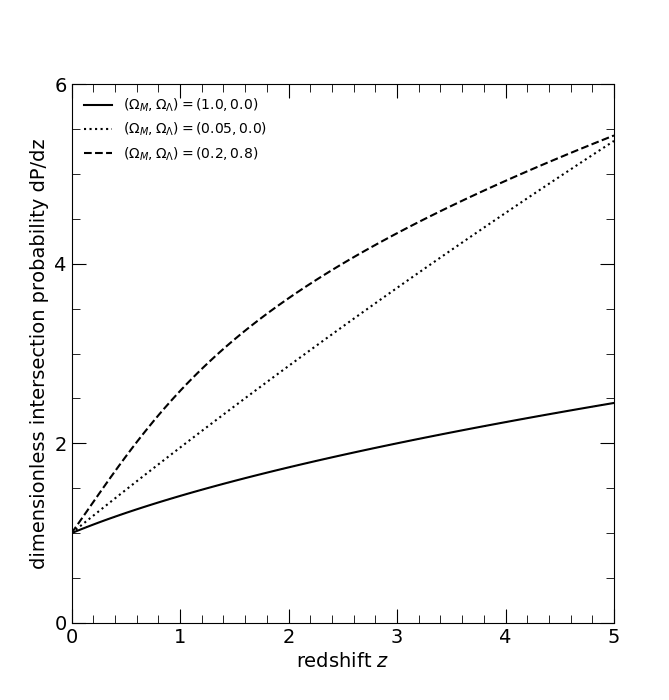
The dimensionless differential intersection probability dP/dz; dimensionless in the sense of n(z) σ(z) DH = 1. The three curves are for the three world models, (ΩM, ΩΛ) = (1, 0), solid; (0.05, 0), dotted; and (0.2, 0.8), dashed.